
Mathematics Software
Development
by Students for Students
Lena Papathomaidi,
Vassilis Ekonomou,
George Bariamis
Doukas School
Mesogion 151, Marousi 151 25
tel: 680 8000,
fax: 680 7420
email: economu@doukas.gr
Abstract
This project was inspired by the constructionist approach and the research by the MIT Instructional Software Design Project group. It is based on the principle that "knowledge structures" are built mainly by the subject (rather than transmitted by the teacher) and that they are realised more efficiently in the form of material structures, as children do with construction sets. Therefore, the notion of programming is re-defined as a source of learning and experimentation based on software design.
In order to study this extended approach to software design we developed a mathematics application for children inspired and designed by other children. During the school year 1995-96 and in particular, from March to June, we implemented a pilot application entitled: "Problems of Proportional-Inverse Amounts". The design group included: a group of 6th grade students, the class teacher, the teachers of informatics, music and arts as well as the software developer. Our aim was for children to take part in all development stages, even at a simple user level.
Keywords
primary education, mathematics, logo programming, constructionism, multimedia.
1 Introduction
During the 1995-96 school year and in particular, between March - June, a pilot programme called "Math Software Design from Students for Students" took place. Grade six students (one section) were chosen for this project. The classroom teacher, the computer teacher, the music and arts teachers and the Programme developer also participated in this project. The objective was for children to take part in all stages of development, even through simple involvement.
Specifically, we tried to maximise student interest and improve co-operation while encouraging them to take initiative through involvement in all levels of software production, according to their aesthetic, logical and cognitive needs. Moreover, there was an effort to develop collaboration between students and the teachers involved and for them to understand programming techniques through use of algorithms and analytic procedures.
Finally, one of our objectives was to try to reverse the dominance of abstract notions in math teaching and to offer, in turn, various concrete elements (from the logic involved in problem-solving to finding solutions through pictorial representation, sound, video and colour).
The following development phases were employed:
2 Working in the Class
The first step was to acquaint children with equivalent fractions, which are necessary prerequisite to understanding ratios. We studied the relationship between proportional numbers and proportional fractions, in a way to help students understand ratios.
The next step was to help them learn about amounts-quantities as well as to discover the relationship (proportional or inversely proportional) existing between these sums (e.g., kilos/drachmas, food/days).
The third step was to present the above relations through math problems (data-desired result), where students discovered and expressed the specific procedure which should be followed to solve these problems. They were assisted by their teacher in this step in order to:
| The above procedure took place in classroom during the lesson on ratios and proportions. With the help of their teacher, students designed their own exercises, which they then, transferred to computers, assisted by their Computer teachers. |  |
Students showed great enthusiasm and interest when they realised that they would create and write math problems and in particular, when they were told their computers would assist them. We were pleased to see that students, who up to then hadn’t shown any particular interest in Mathematics, gladly participated in this project.
3 Working in the Computer Lab
It was during the Computer class that the students’ ideas, plans and proposals materialised. Their expectations were great and often exceeded the limitations of the lesson, namely time but also objective factors. The students wished to get involved at all levels. The Computer teacher had to provide a balance between their expectations and reality, to introduce to concepts, which would help them acquire more basic knowledge (namely, in logic, design, analysis, algorithms, variables and procedure) and finally, to co-ordinate collaboration between the students and the programme developer, math and art teachers without pressuring students to think as adults but trying to bring the adults closer to their way of thinking).
3.1 Teaching of notions: Variables - Procedure
| These notions are fundamental to understanding both the logic in math and programming. These notions are taught regardless of whether students will ever programme (to whatever degree). | 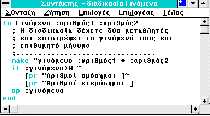 |
3.2 Algorithm Problem Analysis and Design - Logic
The teacher trying to teach a programming language has to teach some elements of logic usually in a confined period of time. Moreover, he has to adapt them to the capabilities of each age group and to the actual needs. This experiment proved once again, the need to give priority to the teaching of technical analysis and problem design, in the algorithmic and logical approach to these issues. Exactly this attempt was made. Children, from the age of approximately 11, are ready to learn the analysis and processing of the logic behind math problems. This may be what we are looking for in Computer classes. Through a "real-life need" (i.e., the desire to build a step-by-step application in order that other children can practice proportions with computer assistance), they learned some elements of Logic in a multi-faceted attempt, which we believe should be a part of what we call "Elementary Computing Education". In general, designing software as an educational procedure, encourages children to inquire, understand and reproduce concepts in mathematics which are usually vague and far-removed from them. Moreover, this procedure supports the need to expand Computer classes and to incorporate realistic needs.
4 Application development
From the initial meetings with students with students, we establish a flow-chart on the basis of which we developed the procedure necessary to create this software application: needs analysis, collection and digitalisation of the material, code implementation and application testing. Moreover, we determined how the students and various teachers involved would work together was to restrict the logistics in organising this project.
4.1 Needs analysis
Firstly, the students were informed about the needs and demands of the project. In other words, they were told about the material to be used, how the data would be managed and applied, how the problems need to be presented, where the answers would be checked and, in general, everything that would be included in this application., the events, which would surround the application.

Students came to the Computer Labs and presented their proposals, discussed and designed the table, the introductory screen, the problem selection screen and in general, how they would present the interface.
We chose the way in which the student-author would "teach" the problem to the computer so that it would be ready for the student-user to solve it (in other words, we stressed the clear phrasing of the problem in identifying, combining and entering the data). Finally, efforts were made to use diagrams on the screen, to better explain the theory behind teaching proportions. It was necessary, at this point, to pool their knowledge of mathematics, music and design.
4.2 Collection of the material
We requested and collected the necessary data for a multimedia application: sounds, tunes, pictures, video, etc., as well as books and notebooks used by students in class.
|
 |
With the assistance of their music teacher, the students used the Windows recorder to record their own sound-effects to accompany the programme. Music from CD-ROMs was also added.
While data was being collected, special emphasis was paid to the criteria that would be used in the selection process, especially since the material is one of the main elements of communicating this application to the users. |
4.3 Programming the application
Following the needs analysis and the collection of the initial material, the implementation of the code began.
Multi-Logo (the Geek version of Comenius Logo) was the platform chosen and used for the development of this application. It is a programming language with a good-sized command library used in multimedia resource management, such as ability to add pictures and move them on the screen, ability to add sound midi files.
One additional element, which contributed to this selection, is the fact that students become familiar with this environment from the first years of Elementary School, during Computer classes.
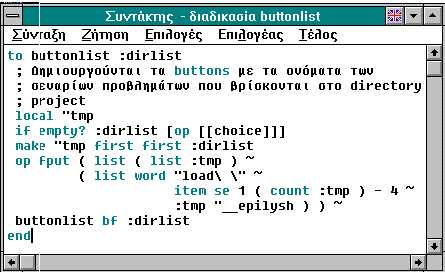
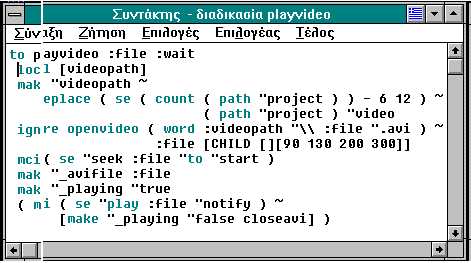
The following procedures
were created:
|
Our aim is to create
"microworlds" within which students will take
initiative to compose their own simple procedures, which
could later be used within a broader environment.
|
4.4 Application testing
After the code was completed, the result was presented in class using a projector and data display. Then, the application was tested by a group of students. Queries were raised and recommendations were made for improvement.
Finally, after the improvements were incorporated both in the design and the "code", the programme was installed in the Novell server of the Computer Labs. Student groups used Windows to insert more than thirty types of ratio problems. At the same time, other groups selected problems, which were already inserted and tried to find their correct solution following the steps they themselves had established according to the model chosen.
4.5 Practical Problems
During the application design, several practical problems arose:
4.6 The next steps...
A different approach was taken for the subsequent steps. Microworlds easy to reach by students were created. I.e., flexible procedures, which students apply immediately were created. The basic points of designing the next steps are as follows:
5 Conclusions
After the application’s completion, the degree and quality of co-operation between students improved considerably. By working in small groups, students had the opportunity to exchange views in a creative way, and participate actively toward a common goal. We also noticed that students were ready and flexible to the project’s demand.
Either working by themselves or assisted by their teachers, students built a step-wise application with concrete objectives. The entire procedure was pleasant for them. Due to their active participation, they learned about algorithms analysis and design. Prior to this, these notions were abstract to them despite their involvement with computers as users.
Throughout all the phases of the project, from material collection to the use and testing of the final programme, students not only learned about programming techniques but about the procedure from the design stage to the materialisation stage. In this way, they realised the interdisciplinary usage of Informatics and the task of the programme developer regarding software production was demystified.
We discovered that children of this age group and with this cognitive ability, are not ready to follow programming tasks. The project showed that though their involvement in high standard programming may not be advisable, their active participation in all the other phases is highly recommended. Moreover, it was proved that the time accorded to this project was inadequate at a cost to creativity and originality. Finally, the need for more assistance in this project, creates problems of design and co-ordination.
The different way in which the math class evolved had positive effects on the students. Their desire to discover and acquaint themselves with new data increased their motivation and interest in this project.
According to the teacher, the project had an effect on the students’ mastery of the topic. This was verified by the promising results on the final exams; this section scored above average.
6 Acknowledgement
We would like to express our thanks to C. Doukas, Y. Kotsanis, Th. Dimos, L. Houda, S. Moraiti and to all students of Grade 6, Section 3, school year 1995-96, for their support and assistance.
References