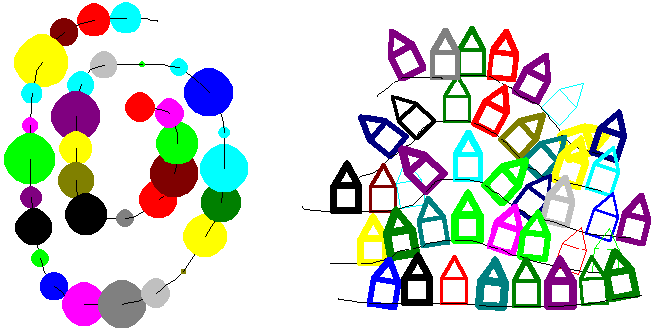I BEG YOUR PARDON TURTLES:
DON’T FORGET ABOUT DATA STRUCTURES
Ivan Kalas with Andrej Blaho
Department of Informatics Education
Comenius University,
842 15 Bratislava, Slovak Republic
tel/fax: + 421 7 724 826,
email: kalas@fmph.uniba.sk
Abstract
Data structures often play an only
second-rate role in Logo literature and practice.
Although there are some excellent Logo books devoted
completely to data structures, these are not considered
to be books for everyone – they are more
academically-oriented advanced courses. Materials for
students and/or beginners often push this topic into a
final chapter with no obvious connection to turtle
geometry.
We believe that Logo data structures
can play natural component in mid-level Logo activities
and try to illustrate that gap between them and turtle
geometry does not need to exist. Instead, in this
apparent gap there are dozens of excellent pure Logo
activities for students-developers.
Keywords
data
structures, Logo, procedural and declarative
representations
1 Introduction
Since the beginning of the development of Comenius Logo
(SuperLogo, MegaLogo, MultiLogo in other countries) and
especially when giving courses and seminars at our university to
future teachers we have had the feeling that data structures in
Logo do not receive enough attention. In many Logo books they
often play an only second-rate role. Materials for students
and/or beginners often push this topic into a final chapter with
no obvious connection to turtle geometry. We believe that Logo
data structures should play natural component in most non-trivial
Logo activities. The gap between data structures and turtle
geometry does not need to exist at all. Instead, in this apparent
gap there are dozens of excellent pure Logo activities for
students-developers.
 Our interest in data structures and their
relationship to procedural structures (programs) has roots in our
Lisp background and has been considerably shaped by [2]2 Neither the authors of that
exceptional book nor us think that deep academically-oriented
approach is necessary for engaging atomic data and more compound
data structures into our concern. Both Lisp (Scheme) and Logo
people consider their tool a powerful medium for exploring and
expressing ideas. Abelson and Sussman in [2]name three mechanisms
for forming and exploring complex ideas:
Our interest in data structures and their
relationship to procedural structures (programs) has roots in our
Lisp background and has been considerably shaped by [2]2 Neither the authors of that
exceptional book nor us think that deep academically-oriented
approach is necessary for engaging atomic data and more compound
data structures into our concern. Both Lisp (Scheme) and Logo
people consider their tool a powerful medium for exploring and
expressing ideas. Abelson and Sussman in [2]name three mechanisms
for forming and exploring complex ideas:
- primitive expressions (to represent
basic entities of the programming language),
- means of combination (to build
compound expressions and data from simple ones),
- means of abstraction (to name
compound objects and manipulate them as units).
In the context of Logo data3
these three mechanisms are represented by atomic data
structures, the mechanism to build compound data out of simpler
ones (list operation
supplemented by sentence, fput
etc.) and the mechanism to give names to compound data (make command supplemented by let, name and the mechanism of
procedures’ inputs). Following two lines illustrate all
three of them (to be studied more deeply later):
? make " melody
(list " L8 " O2 " d " c " 2c.)
? play :melody
Fortunately, modern versions of Logo make it possible to take
data approach built on turtle geometry and thus profit from
well-developed Logo tradition. We are getting much in reward for
this decision:
- visualisation, essential property of
turtle geometry and all active teaching/learning computer
environments (microworlds), see [7],
- inconceivable extension of traditional
turtle geometry activities, see for example [8]
- important essential topics to think about
(and thus build important concepts and develop our
informatics culture). We have to choose suitable
representation for data – proper choice is a
powerful technique for controlling complexity. Moreover,
... whenever we have two different representations of
the same thing we can learn a great deal by comparing
representations and translating descriptions from one
representation into the other.
- Shifting descriptions back and forth
between representations can often lead to insights that
are not inherent in either of the representations alone,
see [1].
To cope with data structures is exciting experience which will
sooner or later make us understand that in Logo there is hardly
any difference between computer program and data.
2 Atomic data are gifts. Compound data are
agreements
Comenius Logo atomic data are words and images.
Words are sequences of characters and images are sequences of
frames (we characterised them in detail in [4]) and Logo provides
us with tools to reach these elements. However, both words and
images represent elementary entities of the language and
logically they are indivisible (any part of a word, i.e. zero,
one or more characters is still a word. Any part of an image,
i.e. zero, one or more frames is still an image). Atomic data
objects serve as building material for more compound data because
they are by themselves not sufficient for many of the problems we
want to cope with. Being the elementary concepts of the language,
atomic data are gifts presented by Logo. Another gift of
the language is a mechanism for building data abstractions, that
is combined data objects representing compound data.

An image used as the default
turtle shape in SuperLogo
Compound data – called data abstractions – elevate
the conceptual level at which we can develop our projects: we
will be talking about and working with points, vectors,
texts, melodies, rectangles etc. These will
be less compound data objects glued together to form single
conceptual units. The gluing mechanism of Logo is enclosing
into a list. This approach might be unusual to some Logo
practitioners: we don’t consider words, images and lists the
Logo data structures. Rather, we consider words and images the
Logo data structures and list a mechanism for building more
complex data structures atop of simpler ones. From the data
structures perspective we consider list to be a verb rather than
a noun: we will list things together. Each compound data
structure will have certain meaning to us and to some primitive
or user-defined procedures – it will be an agreement between
us and some procedures.
In the following chapter we will present a sequence of data
structures of growing conceptual complexity. We will outline
several Logo projects to be further extended by students and
teachers in many possible directions. Many other (easy or
advanced) data structures will not be mentioned here – we
hope that the reader will soon get our message: the mechanism of
data abstraction makes this "sequence" potentially
infinite.
3 Short tour of Logo compound data structures
Our data structures tour will not show any new concepts to
experienced Logo practitioners. Its goal is to illustrate an
alternative viewpoint on data and traditional topics. We want to
make a sample tour for a group of tourist guides to
attract their attention to places which may latter be of interest
for future tourists in their groups. Our vehicle will be
the mechanism for building data abstractions and treating new
compound objects directly as objects, not as a compositions of
their parts.
3.1 Points
They will prevent us from forgetting that turtle geometry is
not the only possible representation of geometric phenomena in
Logo. A point is created by gluing together (listing
together) two atomic data objects, the x and y co-ordinates of the
corresponding point in the graphics screen. It is very important
to realise that a point is more than two numbers, a point
is one compound object, not two separate numbers, thus we can
give it a name:
? make " P1 pos
We will treat it as one piece of complex data. There are
several primitive procedures that accept this agreement. Except
the pos operation
which outputs a point, there are other procedures
(primitive or user-defined) that expect points as their
inputs:
? setpos :P1
Although there are Logo tools to obtain two parts of a point
or to construct a point out of x
and y
co-ordinates, procedures like setx
and sety do not
understand the abstract notion of points, they are not a
partner in this agreement.
3.2 Time
Let us study another compound data object, an output of the time primitive
operation:
? sh time
[21 35 2 49]
It is a composition of four numbers representing hours,
minutes, seconds and hundredths of a second. Obviously, not all
lists of four numbers are times. For example, [25 -7 72 5] would not
be accepted by any time processing procedure. Similar to points,
we can name a time and pass it to a procedure:
? make " T1 time
? sh :T1
[21 37 10 63]
? sh time.plus :T1 [0 30 0 0] ; What time will be half an
hour later?
[22 7 10 63]
It is not trivial to define correctly time algebra,
i.e. operations like time.plus
or time.difference.
Usually, such definitions have to go inside the compound data
objects. However, it is not important from outside. From
outside, these procedures are just getting and/or producing time
objects.
An alternative way how to represent time – or even more,
the flow of time – is traditional clock with three (or
four!) hands. Let us develop a simplified command to visualise
the flow of time by rotating the seconds hand:
to show.time
setpc 0 setpw 20 pd fd 0 ; Draw a dot in the middle.
px ; Set penreverse mode.
setpc bg ; Make pen colour equal to the background.
seth 6 * item 3 time
setpw 2
draw.seconds.hand
show.seconds time
end
to show.seconds :now
if heading <> 6 * item 3 :now ~
[draw.seconds.hand ~
rt 6 ~
draw.seconds.hand]
show.seconds time
end
to draw.seconds.hand
fd 60 pu bk 80 px fd 20
end
Several further developments are possible here:

the clock should control three independent
hands (or even the fourth one for visualising the hundredths of a
second – this experiment is worth trying),
- three hands may be more transparently
controlled by three turtles. Soon, we will present a view
on multiple turtles as repositories of data,
- if the clock is depicted by turtles, there
is no reason to stick the clock to one fixed place –
why not to drag it atop of the world map with time zones
so that the actual time shift is visualised,
- we can add a nice clock face, either
regular or irregular, making use of traditional Logo
turtle drawing tools.
3.3 Melody – a list of unknown
length
Points are lists of two numbers, times are lists
of four numbers. Other data object may, however, contain unknown
(variable) number of items. An example of such object is a melody:
? make " Yesterday
~
[I21 T80 L8 O2 d c 2c. P e f# g# a b O3 c O2 b. 16a 2a. P ~
a a g f e d L4 f 8e e. d c 8e 8d d. O1 8a O2 c 8e 8e 2e]
? play :Yesterday
This list of words specifies the instrument to be used to
perform the melody, its tempo, the default notes’
length, octave specification, pauses and, obviously, the notes
themselves. Most important about melodies is that the play command
understands them and can perform them. Moreover, melodies
can be constructed, processed or modified by Logo procedures:
? play (se :Yesterday
[I40 T70] bf bf :Yesterday)
And yet another key point: due to its unknown length, to
process a melody in a certain way may require a recursive
approach. The reason is that melody inherently is a
recursive data structure:
- the empty list []
is a melody,
- if :A is
an acceptable word (not to be specified here) and :M is a melody,
then fput :A :M
is a melody.
Recursion is a usual control structure to cope with lists of
things. If we are to replay the same melody on different
instruments (specified by a list of instruments like [I73 I20 I32 I4 I45])
we may do it in the following way:
to replay :melody
:instruments
if empty? :instruments [stop] ; We suppose that melody
contains no
play fput first :instruments ~; instrument specification
itself.
:melody
replay :melody bf :instruments
end
3.4 Text
Let us agree that:
- any Logo word is a text,
- if w1, w2, ... are Logo words then [w1 w2 ... ] is a text.
 Texts are exciting data objects because
turtles can type them in any specified font, colour (identical
with the turtle’s actual pen colour), heading, position,
style and size in the graphics screen. The setttext (set turtle text)
primitive command is equipped with a chooser to specify directly
all technical settings (without knowing the fonts names, styles,
sizes etc.). The ttext
command takes a text and makes each active turtle print it
at its actual position and heading:
Texts are exciting data objects because
turtles can type them in any specified font, colour (identical
with the turtle’s actual pen colour), heading, position,
style and size in the graphics screen. The setttext (set turtle text)
primitive command is equipped with a chooser to specify directly
all technical settings (without knowing the fonts names, styles,
sizes etc.). The ttext
command takes a text and makes each active turtle print it
at its actual position and heading:
? repeat 5 ~
[maketurtle repcount ~
se [200 150] - random [400 300] ~
random 360]
? tell [1 2 3 4 5]
? each [setpc random 15]
? settt [Arabia] [22 700 0]
? ttext [Let us Logo!]
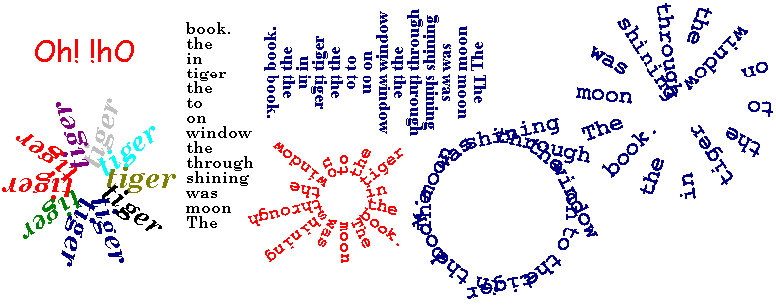
When supported by the textsize
operation, the text typing commands offer dozens of
complex Logo activities, see the figure bellow. Many of them may
be used to illustrate essential concepts of text processing,
informatics and DTP. They give us the chance to make many
unintended mistakes and discoveries with words rotations,
colours, mirrors, margins, columns, texts aligned to
curves etc. And more: as far as texts are composed of
words and words are composed of characters (which are words as
well), a lot of serious thinking will be done by students before
they manage to align a text on the circle from outside, from
inside etc. – a lot of serious work within amusing topic.
3.5 List of angles
 If we use the list mechanism to glue together
several angles (without fixing their number), several bizarre
Logo procedures may be developed to handle and visualise such
data objects. In [5] G. Futchek describes an excellent method for
generating random mazes based on an input list of angles.
A turtle (with its pen down) will pick at random one of the
angles and turn that much right. Then it will move by fd 10 – unless the
turtle has already visited that point. If this is the case, the
turtle will pick another angle and try again, until all possible
choices (angles) were applied from all reachable points
within an area specified by a user-defined outside.area? predicate. To
implement this strategy, the shuffle
Logo primitive operation is extensively used (although Futchek in
[5] presents several clever user-specified shuffling techniques
– worth trying!):
If we use the list mechanism to glue together
several angles (without fixing their number), several bizarre
Logo procedures may be developed to handle and visualise such
data objects. In [5] G. Futchek describes an excellent method for
generating random mazes based on an input list of angles.
A turtle (with its pen down) will pick at random one of the
angles and turn that much right. Then it will move by fd 10 – unless the
turtle has already visited that point. If this is the case, the
turtle will pick another angle and try again, until all possible
choices (angles) were applied from all reachable points
within an area specified by a user-defined outside.area? predicate. To
implement this strategy, the shuffle
Logo primitive operation is extensively used (although Futchek in
[5] presents several clever user-specified shuffling techniques
– worth trying!):
to maze :angles
maze1 shuffle :angles
end
to maze1 :options
if empty? :options [stop]
rt first :options
pu fd 10 ; Go and test if already visited.
test or ( dotcolor = pc ) ~
outside.area? pos
bk 10
iff [pd fd 10 maze1 shuffle :angles bk 10]
lt first :options
maze1 bf :options
end
Two points here are of our main concern now:
- the outline of the final maze is specified
by the outside.area? predicate, thus the outline itself is in a way
represented by this user-defined procedure. A simple
modification of the maze and maze1 commands would be to send them also the second
input – the name of the outline-specifying
predicate, or even its definition list (see
later). However, a question then arises: Is there any
difference between the list of angles and the outline-specifying
predicate from the data perspective? Later we will
see that Logo procedure may be considered a regular data
structure,
- due to repeated shuffling of the input,
the list of angles represents the resulting maze
in an ambiguous way. Although this fact has some
unpleasant theoretical consequences for Lisp-like
languages, we appreciate random choices in turtle
geometry very much!
3.6 List of Logo instructions
Certain lists of words (or even lists of lists and words) have
very special structure – they resemble Logo instructions,
for example [fd 50 rt 45]
or [if :in? [fd 50] [bk 50]].
There is a procedure which understands such lists and is able to run them as if they
were true pieces of Logo programs:
? make " P1 [fd
100]
? run :P1
? :P1
Message: I don’t know what to do with [fd 100]
? repeat 4 [run :P1 rt 90]
The latest line is extraordinary! It combines usual command
with running a value of P1!
It seems like there is no difference between instructions and lists
of instructions when run (evaluated) by run. In fact, for Logo an
instruction in the command line is internally represented by a
list containing that instruction or instructions. Logo itself is
represented by the run
command, it internally runs instructions using the run command. It is essential to
let our students realise that we have already encountered lists
of instructions many times:
? repeat 5 [fd 150 rt
144]
? if :N > 10 [rt 75] [rt 45]
? make " i1 [rt 75]
? make " i2 [rt 45]
? if :N > 10 :i1 :I2 ; Are the following 3 lines
identical?
? if :N > 10 [run :i1] [run :i2]
? if :N > 10 [run [rt 75]] [run [rt 45]]
The second input to repeat
structure is a list of instructions, the second and the
third (optional) inputs to the if
conditional statement are such lists. Therefore we can easily
define the following control structure:
to forever :what
run :what
forever :what
end
? forever [fd 40 - random 80 rt random 5]
However, this is something very exceptional, it is a
revolution in our traditional understanding of programs and data!
In fact, some data objects are programs. Later we will see that
each piece of program is a piece of data. There is no difference
between them and we will build on this discovery several times
later on.
3.7 Polygon list
If we type in repeat 4
[fd 100 rt 90], the turtle (in fact, all active
turtles) will draw a square. We already know that the list [repeat 4 [fd 100 rt 90]]
means the same. However, while the first instruction is
considered a procedural representation of a square, the
second one is its declarative analogy. Another declarative
representation of the same square would be a list [100 90 100 90 100 90 100 90] if
only we acquire an agreement that the first item of the list
means go forward 100, the second item means turn right
90 degrees, the third item go forward 100 etc. We can
go even further (or deeper) and accept the repetition factors
in such lists: [30 60 5 [50
10] 20 90] would mean go fd 30, turn rt 60,
repeat 5 times (in the same way) the list [50 10], then go fd 20
and turn rt 90. Obviously, inside the inner list another
list may occur ... etc. Let us call such structures polygon
lists:
- the empty list [] is a polygon
list,
- if a1 and a2 are numbers and [a3 a4 ... ] is a polygon list, then [a1 a2 a3 a4 ... ] is also a polygon list,
- if r1 is a
non-negative number and [a1 a2 ... ], [b1
b2 ... ] are polygon lists,
then also [r1
[a1 a2 ... ] b1 b2 ... ] is a
polygon list.
We can study several properties of a polygon list (its
total length etc.) and we can define a command to correctly
interpret it in a corresponding turtle geometry way:
to do.it :l
if empty? :l [stop]
test number? item 2 :l ; Which alternative?
ift [fd first :l rt item 2 :l]
iff [repeat first :l [do.it item 2 :l]] ; Repetition factor
...
do.it bf bf :l ; Go on with the rest
end
These polygons are represented
by the followingpolygon lists:
[10 [2 [9
[10 10] 0 90] 0 36]]
and
[3 [20 90 160
-90 20 -90 160 90] ~
20 90 160 -90 20 -90 ~
3 [20 -90 160 90 20 90 160 -90] ~
20 -90 160 90 20 90]
Fortunately, there are also two primitive commands that
understand polygon lists and can interpret them very fast:
polygon and polygonline (the first
one also fills the polygon in actual filling colour). Several
advanced data processing operations can be defined (e.g.
transforming a turtle geometry command into a corresponding polygon
list). The most important here for us is that polygon
lists contain lists which contain lists etc. They are
recursive structures par excellence.
3.8 List of turtles
In any version of Logo with multiple turtles we are getting
new and interesting data structure: the turtles themselves. The
reason is that each turtle represents several pieces of data (not
always atomic) in itself: through its name, its home and actual
positions, basic and current headings, pen state, filling colour
and active shape colour, its shape, actual frame and animation
mode, its actual font etc. In fact, turtles are rather compound
data structures by themselves. When combined with other data
structures and techniques, multiple turtles (practically
unlimited in their number) provide Logo users with exceptional
palette of possibilities. Let us examine some of them.
3.8.1 List of turtles to be created
Let such structure be a list of the form [[name [x y] h] [name [x y] h]...]
where each sublist represents a turtle to be created by the maketurtle command.
First item of the sublist specifies its name, the second one
specifies its home position and the last one its basic heading.
To illustrate different data processing approaches, we show three
equivalent definitions of a command to interpret the list:
to create.them :list
if empty? :list [ask all [st] stop]
let "it first :list
maketurtle first :it se item 2 :it item 3 :it
create.them bf :list
end
to create.them :list
map [[it][maketurtle first :it se item 2 :it item 3 :it]]
:list
ask all [st]
end
to create.them :list
local "it
foreach "it :list [maketurtle first :it se item 2 :it
item 3 :it]
ask all [st]
end
3.8.2 List of names to be asked to do ...
Any subset of all turtles may be given a name. Later we can
use the name (of the list of turtles’ names) to ask them to
run a list of instructions:
? make " girls
[jenny marta sueli]
? make " to.do [repeat 10 [fd 10 rt 110 fd 5 lt 110]]
? ask :girls :to.do
We could have done the same by saying ask [jenny marta sueli] [repeat ... ].
3.8.3 Images and shapes to visualise data
As far as any turtle may take any image as its shape , we can
develop very exceptional modifications of well known recursive
curves of level N.
Let us consider the famous Hilbert curve and implement it in the
following way: turtle 0
– with its pen up – will move forward according to the
usual Hilbert recursive strategy. However, instead of drawing a
line, it will create several turtles: one per each elementary
line segment Therefore, the final composition will look like
usual Hilbert curve, but will contain 4*:N+3 turtles instead of single
piece of line. All turtles will have the same shape of 24 frames – a line
segment rotated around a point into 24 different directions, see
above. Thus, we built the curve out of the turtles’ bodies
themselves! The turtles now represent the Hilbert curve by
themselves (by their shape, positions and headings). This is an
exciting example of turtles as data structures!

to hilbert :l
erturtle all cs gs
maketurtle 0 [50 -100 0]
tell 0
pu
let "c 1
hilbert1 :l 1
erturtle 0
tell all
end
to my.fd :a
maketurtle :c se pos heading
ask :c [setshape :hilbert st pu]
make "c :c + 1
fd :a
end
|
to hilbert1 :l
:p
if :l < 0 [stop]
lt :p * 90
hilbert1 :l - 1 ( - :p )
my.fd 20
rt :p * 90
hilbert1 :l - 1 :p
my.fd 20
hilbert1 :l - 1 :p
rt :p * 90
my.fd 20
hilbert1 :l - 1 ( - :p )
lt :p * 90
end
|
Turtles may represent serious bulks of data by their shapes
– data which cannot be easily represented by any other
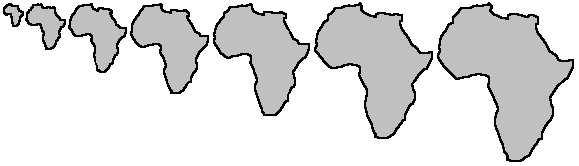
(traditional) means. For example, think about a map of a
continent where each state is visualised by a turtle! To decide
to which country a point belongs (clicked in the graphics screen
by mouse) becomes a trivial task.
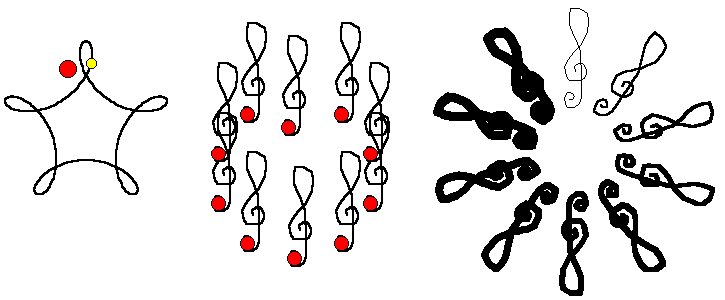
This is famous Hilbert curve of the level 3
composed of 63 turtles. As far as all of them are active,we can
let them turn by rt
30 (the second figure), thenonce more rt 30 (the
third figure), and once more rt 30 (the last
figure).The figure used at the first page of this paper is a
result of saying back
10to all Hilbert turtles when they are
in their home positions and basic headings.
3.8.4 Levels of turtles

One of the attributes of multiple turtles is their age, i.e.
the order in which we created them. The age of turtles also
defines the order of turtles' shapes when they overlap on
the screen while moving: the younger the turtle is, the fewer
turtles can cover it with their shapes. The youngest turtle is
always on the top of all others. Let us develop a small project
by creating a row of 10 turtles-houses named house1, house2, ... with small gaps in
between. There will be another turtle – the animation turtle
Tomash riding a
bike, thus moving forward at the same line with the houses. Let Tomash be the youngest
of all turtles, therefore he will overlap all houses while
moving. However, we can redefine the age of already existing
turtles by the reorder
command and thus develop the following animation effect: if we
click a house, we will let it become younger than Tomash – he will now move
behind it. If we click the same house once more, the order will
change once more and Tomash
will move in front of it. To implement this behaviour we will
maintain two levels of houses: the older ones than Thomas and the younger
ones. Whenever we click a house, it will be moved from olders to youngers or the other
way round:
to in.row
erturtle all cs gs
repeat 10 [maketurtle word "house repc [-150 0] + repc *
[45 0] ~
ask word "house repc [setshape pick :houses st]]
let " olders all
let " youngers []
maketurtle "Tomash [-220 0 90]
ask "Tomash [setshape :bicycle ~
setframemode "true ~
setframe 1 ~
pu st]
move
end
to move
if key? ~
[case readkey ~
[27 [stop] ~
0 [if member? touched se :olders :youngers ~
[change.age touched]]]]
ask "Tomash [setframe frame + 2 fd 2]
wait 50
move
end
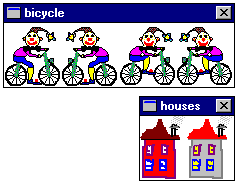 to change.age :it
to change.age :it
if member? :it :olders ~
[make "olders butmember :it :olders ~
make "youngers fput :it :youngers] ~
[make "olders fput :it :olders ~
make "youngers butmember :it :youngers]
reorder ( se :olders "Tomash :youngers )
end
It would be easy to extend the in.row project so that whenever
we click Tomash
instead of a house, he will do the about turn.
3.8.5 Screen animation agenda
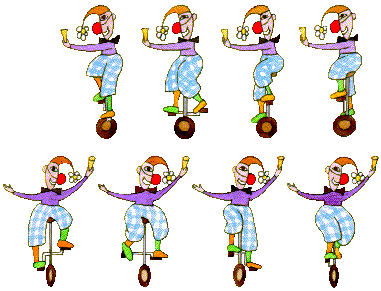 Tomash created above is an
animation turtle. As an alternative to basic turtles, animation
turtles allow us to change the frames of their shapes at any time
with the setframe
command. However, when we obtain or create nice multiple-frame
images depicting complex movements of a character in all possible
directions, we have to somehow control the turtle’s
trajectory around the screen, i.e. we have to represent a kind of
animation agenda to specify the exact headings of the
movement, basic steps, shapes and frames of the turtle etc. Such agenda
may be a list of the form:
Tomash created above is an
animation turtle. As an alternative to basic turtles, animation
turtles allow us to change the frames of their shapes at any time
with the setframe
command. However, when we obtain or create nice multiple-frame
images depicting complex movements of a character in all possible
directions, we have to somehow control the turtle’s
trajectory around the screen, i.e. we have to represent a kind of
animation agenda to specify the exact headings of the
movement, basic steps, shapes and frames of the turtle etc. Such agenda
may be a list of the form:
[[heading step distance
wait.time shape] ... ] for example:
[[135 2 120 50 :tomash.south.east] ... ]
and should be interpreted by a user-defined agenda-agent.
Sometimes we have to involve similar planning for several
animation turtles moving in parallel (taking into account exact
timing, mutual interactions etc.). More complex agenda is
needed then.
3.9 Sequence of keys
Let us implement a simple command which reads the keyboard and
makes the turtle move North 10
steps (if the n
key was pressed), move East 10
steps (if the e
key was pressed) etc. In a way, the move command works with sequences
of keys, a kind of special codes or representation
of certain turtle drawings. Therefore, it is straightforward to
modify the command so that it understands and interprets a given
list of letters (as if keys pressed on the keyboard):
to move
case readchar ~
[n [seth 0 fd 10] ~
e [seth 90 fd 10] ~
s [seth 180 fd 10] ~
w [seth 270 fd 10] ~
q [stop] ~
[sound [550 20]] ] ; Else ...
move
end
|
to move.it :l
if empty? :l [stop]
case first :l ~
[n [seth 0 fd 10] ~
e [seth 90 fd 10] ~
s [seth 180 fd 10] ~
w [seth 270 fd 10] ~
[sound [550 20]]]
move.it bf :l
end
|
Let us go on: we can give names to certain sequences (lists)
of keys, thus start to build a kind of library of shapes.
For example:
? make " step [n n
w s e e n]
We can also modify the move.it
command so that it accepts more complex sequences: beside n, e, s and w letters it may contain the
names of other sequences, like [step
s s step s s step s s step]:
to move.it :l
if empty? :l [stop]
case first :l ~
[n [seth 0 fd 10] ~
e [seth 90 fd 10] ~
s [seth 180 fd 10] ~
w [seth 270 fd 10] ~
[move.it thing first :l]]
move.it bf :l
end
Now, there is no reason not to try this:
? make " steps [n n
w s e e n steps]
? move.it :steps
We have just created a surprising method of defining infinite
recursive computation (drawing) through certain lists of words!
If we wanted to elaborate even more, we would introduce a
conditional tool to stop the infinite drawing, thus developing a
complex declarative language representing certain Logo
recursive drawings.
3.10 List of points. Vectors. Lists of
vectors
We have already discussed points, let us now collect
several points into a list. We can, for example, define an
operation which recognizes the left mouse button’s clicks
and collect the actual positions of the mouse cursor into a list:
to
collect.points
op reverse collect.points1 []
end
|
to
collect.points1 :l
case readkey ~
[27 [op :l] ~
-2 [make "l fput mouse :l]]
op collect.points1 :l
end
|
In this way, we can represent outlines of states or continents
or various drawings, which can later be re-drawn without any
changes or modified in one of many possible ways. Bellow we see a
sequence of repeated transformation which deletes points which
are too close to each other within the list of points.
However, a list of points [P1 P2 ... ] is still only a list
of points: we cannot reproduce the same drawing at different
positions within the screen, we cannot reproduce it turned right
by 45 degrees
etc. – we cannot overcome the basic properties of Cartesian
co-ordinate system. What we definitely can do is to shift it into
different representation – vector representation. And it is
worth doing because (beside other nice properties of this
alternative form), vectors are directly supported by SuperLogo. A
vector is defined as a collection of all equivalent
directed line segments. This concept coincides with the fact that
in Logo we can consider a point P
as:
- a position in the graphics screen,
- any displacement identical in direction
and magnitude with the displacement of P
from the origin.
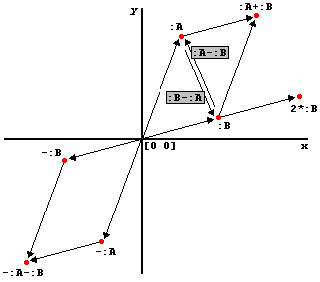
We can say:
? make " A [20 50]
? make " B [35 10]
then Logo will understand correctly expressions like :A+:B, 2*:B, :A-:B, :B-2*:A, 0.2*:B etc. – we are taking
a serious step towards abstraction: we and Logo accept the
concept of a vector as a single object, not the list of
two co-ordinates. Our turtles will understand expressions like ask [Jenny Marta Sueli] [each
[setpos pos + :A]] making these three turtles walk
along the vector :A
from their actual positions etc.
to do.points :l
if empty? :l [stop]
setpos first :l
pd
do.points bf :l
end
|
to
points.to.vectors :l
if empty? :l [op []]
if empty? bf :l [op []]
let " v (item 2 :l) - first :l
op fput :v points.to.vectors bf :l
end
to do.vectors :l
if empty? :l [stop]
each [setpos pos + first :l]
do.vectors bf :l
end
|
points.to.vectors
operation transforms list of points into a corresponding list
of vectors, do.vectors
makes each active turtle realise such list starting from its
actual position. A lot of usual vector transformations can be
involved in this operation. If the turtles are named 1, 2 … etc., then each [setpos pos + first :l]
line can be replaced e.g. by
each [setpos pos + (9 +
who)/10 * first :l]
thus resizing the original drawing by factors 1, 1.1, 1.2 … etc. Beside usual
vector operations Logo also offers some more advanced ones. For
example, we can directly rotate a vector clock-wise around the
origin by a given angle. A point (i.e. a vector) obtained by
rotating point (i.e. vector) :P
by :n degrees
will be denoted by :n/:P.
 Therefore,
if we create a planet with its home position in e.g. [150 0] and its shape
being item 2 :planets,
then to let it rotate forever around the origin we just say forever [setpos 1 / pos].
If we create 20
turtles named 1, 2 … etc. at the
same position [150 0],
by saying forever [each
[setpos who / pos]] we let them rotate at different
speeds. We can also let one turtle (the Moon) rotate around
another turtle (the Earth) which rotates around the origin (the
Sun). We can easily specify two different speeds as two inputs
for Eart.and.Moon
command:
Therefore,
if we create a planet with its home position in e.g. [150 0] and its shape
being item 2 :planets,
then to let it rotate forever around the origin we just say forever [setpos 1 / pos].
If we create 20
turtles named 1, 2 … etc. at the
same position [150 0],
by saying forever [each
[setpos who / pos]] we let them rotate at different
speeds. We can also let one turtle (the Moon) rotate around
another turtle (the Earth) which rotates around the origin (the
Sun). We can easily specify two different speeds as two inputs
for Eart.and.Moon
command:

to Earth.and.Moon
:E.speed :M.speed
ask "Earth [setpos :E.speed / pos]
let "E.pos ask "Earth [pos]
let "M.temp :E.speed / ask "Moon [pos]
ask "Moon [setpos :E.pos + :M.speed / ( :M.temp -
:E.pos )]
Earth.and.Moon :E.speed :M.speed
end
We can also let both planets rotate around a point different
from the origin, that is, we can shift our Solar system by a
vector :A.
Powerful transformations can be obtained by rotating a complete list
of vectors by different angles. We can hardly imagine another
data structure in Logo as potent as vectors. And yet, here
it comes:
3.11 Logo procedure
We have already worked with a concept of list of
instructions which has considerably demolished our
understanding of the differences between data and program. Each list
of instructions can be run (evaluated) as a piece of program.
We have also used the mechanism to name such list and referred to
it later by the name. This is ordinary with ordinary data. This
is also common with procedural objects: we define commands and
give them names. In this way a student (Logo newcomer) defines,
for example, simple commands like my.dot or my.house – elementary
commands without any input to draw a simple object. They may look
similar to the following definitions – either with the repeat or not, it is
not important now:
to my.dot
setpc random 15
setpw 5 + random 50
dot
end
|

|
to my.house
setpw 1 + random 8
setpc random 15
repeat 4 [fd 50 rt 90]
fd 50
rt 30
repeat 2 [fd 50 rt 120]
end
|

|
As far as we do not believe any more that data and programs
are different, we will accept that the name of a user-defined
procedure may serve as an input to another procedure. This fact
provides us with a powerful tool: we can use user-defined
commands in a very complex way, thus offering a Logo beginner
highly stimulating experience: several microworlds can be
developed for the student to discover basic ideas of
turtle geometry yet doing complex things –
beginner’s first steps can be set into seriously rich
environment. To illustrate this idea let us develop a KidPix-like
scribbling tool by mouse: the elementary free-hand drawing
procedure (provided by the microworld) will take one input –
the name of a user-defined command (like my.dot or my.house) and use it repeatedly
while the student draws a free-mode line:
to scribble :proc
cs gs
tell 0
window pu
let "P [0 0]
scribble.loop :proc
endto my.run
:proc
seth towards mouse
lt 90
run ( list :proc )
setpc 0 setpw 1
pu setpos mouse pd
end
|
to scribble.loop
:proc
case readkey ~
[27 [stop] ~
0 [pu setpos mouse pd ~
make "P mouse] ~
-1 [setpos mouse ~
if abs :P - mouse > 30 ~
[my.run :proc ~
make "P mouse]]]
scribble.loop :proc
end
|
Although many modifications of the scribble.loop can be defined,
this one just uses the user-defined command :proc, then resets the previous
pen colour, pen width and position so that no special
restrictions are put on the student’s commands. In the next
figure we see the result of free-hand drawing by scribble " my.dot and scribble " my.house.
However, we can go much further in this direction: instead of
just using the user’s command, our microworld can
first process it and then use it. Not only the
user-defined procedure’s name is a piece of data, also the
procedure’s definition itself is! Indeed, Logo user-defined
procedures are internally represented as lists of lists of
instructions. We will call this structure a definition list.
And there are Logo primitives which know this structure very
well: text and define:
? sh text " my.dot
[[][setpc random 15][setpw 5 + random 50][dot]]
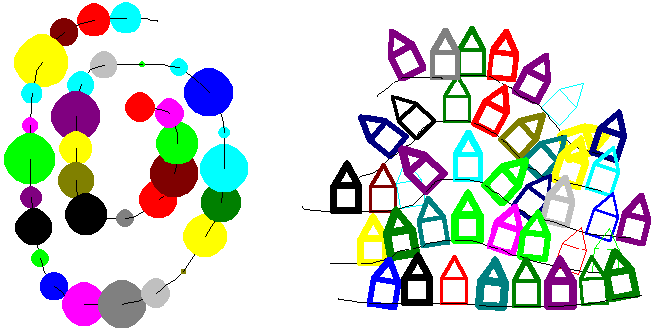
It is well known that the first line (first list within the definition
list) is a list of all inputs names. The crucial thing here
is that the definition list can be processed by other Logo
list processing tools, thus yielding a mutated definition list
which may be turned by the
define command into a proper Logo procedure (or even applied
directly as a piece of program by the apply command!). Let us think
about even simpler user-defined version of my.house command (without setpc and setpw commands). As
far as its definition list is a Logo list (of lists of
words and/or lists), a lot of exciting transformations can be
exercised on it, e.g.:
- all occurrences of fd or forward can be replaced by another word, e.g. tricky.fd. We can define several versions of the tricky.fd command to provide the student with different
funny forwarding, see bellow,
- each constant input to fd or
forward commands can be
parametrised so that random resizing of the drawing (e.g.
of the house) can be performed,
- the outline of the drawing can be computed
in advance and (using polygon
command) filled by the background colour prior the
drawing itself is done (thus making it opaque).
to modify :proc :words :new
if not defined? :proc [stop]
op modify.it text :proc :words :new
end
to modify.it :l :words :new
if empty? :l [op []]
if word? :l ~
[if member? :l :words [op :new] ~
[op :l]]
op fput modify.it first :l :words :new ~
modify.it bf :l :words :new
end |
to tricky.fd :s
let "p pos
let "h heading
repeat 4 ~
[rt 4 - random 9 ~
fd :s + 4 - random 9 ~
rt 180]
pu setpos :p pd
seth :h
fd :s
end |
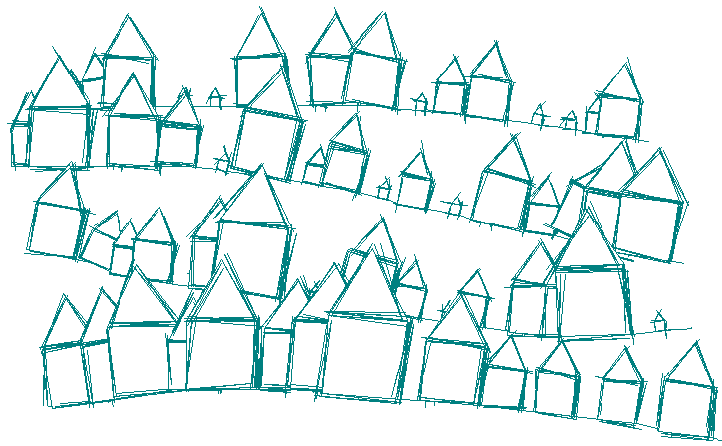
The modifications done in this way may result in exciting and
surprisingly rich shapes. The rows of houses to the right were
obtained by scribbling a mutation of my.house command: the scribble command has
first modified the definition list of my.house by all three
transformations mentioned above. Each fd and forward has been replaced by tricky.fd (defined
above) by:
modify " my.house
[fd forward] " tricky.fd
The modified definition list was not run by run command in the scribble.loop, but applied
to an empty list of inputs by:
apply :new.def.list []
3.12 Logo PowerPoint-like screens
As the concluding stopping place of our Logo data
structures guided tour we want to mention the presentation
of this paper. A Logo project (we call it Logo PowerPoint) is
used to get and visualise the description of each
"page". The page itself is a compound mixture of:
- texts (with several style parameters),
- lists of instructions describing events
which should happen when appropriate,
- references (by name) to other Logo
projects (libraries) which are loaded to illustrate the
material described. These libraries consist of Logo
procedures, variables and turtles, and are erased when
not needed any more,
- turtles to implement Windows-like buttons,
screen animations and all special effects.
- In fact, these pages portray multi-level
compound data objects which conquer the traditional
distinction between active programs and passive data.
4 Open projects must rely upon data
In [7] we specified three important principles of active
learning environments, or microworlds. We claimed there that interactivity,
visualisation and openness should be present in
each microworld to the highest possible extent as far as these
are crucial properties to create learning atmosphere. By openness
of a microworld we understand the extent at which a user can
modify it. We suggested to distinguish three levels of openness:
(1) openness at the level of data, (2) at the level of
usage, and (3) at the level of the type of assignments.
Obviously, for a microworld to be open at level (1), data are
essential to represent other numbers, lists of other objects,
other screens and images, other animations, procedures, sounds
and video, other turtles, other Logo libraries… We find it
very important that learners-developers should acquire a clear
understanding of what such modifications are: new screen, new
assignment, new behaviour means new data somehow represented in
certain data structures.
5 Conclusion
Here follows the list (always those lists!) of reasons
why we find data structures important, natural and inevitable
part of so many Logo creative activities:
- they belong to fundamental concepts of
informatics and computer, they clarify that working with
computer (in very broad sense) means accepting certain
exact rules, agreements,
- they give us a means to explore the same
objects from different perspectives, through different
representations and thus obtain ... insights that are
not inherent in either of the representations alone,
see [1],
- they give us a way to cope with complex
problems. Data structures help to elevate the conceptual
level at which we can design our projects. To avoid data
structures would mean to restrict the palette of topics
to nearly nothing. On the other hand, involving data
structures opens unexpected horizons of attractive Logo
activities with never-ending inspirations,
- they help us to earn a new perspective on
the relationship between data and program,
- they are essential means to develop open
Logo projects.
References
- Abelson, H. and diSessa, A.A.: Turtle
Geometry. The Computer as a Medium for Exploring
Mathematics. The MIT Press, Cambridge, MA 1980
- Abelson, H. and Sussman, G.J.: Structure
and Interpretation of Computer Programs. The MIT Press,
Cambridge, MA 1985
- Blaho, A., Kalas, I. and Tomcsanyi, P.:
Comenius Logo: Environment for Teachers and Environment
for Learners. Proc. of EuroLogo 93, Athens, Supplement
pp. 1 – 11, 1993
- Blaho, A. and Kalas, I.: Playing,
Developing and Computing With Images in Comenius Logo for
Windows. Proc. of EuroLogo 95, Birmingham, pp. 15 –
19, 1995
- Futchek, G. and Schauer, H.: Exploring
Recursion: from Random Walks to the Design of Mazes.
Proc. of EuroLogo 93, Athens, pp. 105 - 112, 1193
- Harvey, B. and Wrigtht, M.: Simply Scheme
– Introducing computer science. The MIT Press,
Cambridge, MA 1994
- Kalas, I. and Blaho, A.: New
Implementation of Logo Opens What Should be Open
(Developing and Implementing Active Learning
Environments), Komputer w Edukacji, No. 2, pp. 5 –
14, 1995 (in Polish)
- Tomcsanyiova, M. and Tomcsanyi, P.:
Experimental IT Education for Lower Secondary School
Using Windows and Comenius Logo. To be found in the Proc.
of EuroLogo 97, Budapest, 1997
 Our interest in data structures and their
relationship to procedural structures (programs) has roots in our
Lisp background and has been considerably shaped by [2]2 Neither the authors of that
exceptional book nor us think that deep academically-oriented
approach is necessary for engaging atomic data and more compound
data structures into our concern. Both Lisp (Scheme) and Logo
people consider their tool a powerful medium for exploring and
expressing ideas. Abelson and Sussman in [2]name three mechanisms
for forming and exploring complex ideas:
Our interest in data structures and their
relationship to procedural structures (programs) has roots in our
Lisp background and has been considerably shaped by [2]2 Neither the authors of that
exceptional book nor us think that deep academically-oriented
approach is necessary for engaging atomic data and more compound
data structures into our concern. Both Lisp (Scheme) and Logo
people consider their tool a powerful medium for exploring and
expressing ideas. Abelson and Sussman in [2]name three mechanisms
for forming and exploring complex ideas:

 Texts are exciting data objects because
turtles can type them in any specified font, colour (identical
with the turtle’s actual pen colour), heading, position,
style and size in the graphics screen. The setttext (set turtle text)
primitive command is equipped with a chooser to specify directly
all technical settings (without knowing the fonts names, styles,
sizes etc.). The ttext
command takes a text and makes each active turtle print it
at its actual position and heading:
Texts are exciting data objects because
turtles can type them in any specified font, colour (identical
with the turtle’s actual pen colour), heading, position,
style and size in the graphics screen. The setttext (set turtle text)
primitive command is equipped with a chooser to specify directly
all technical settings (without knowing the fonts names, styles,
sizes etc.). The ttext
command takes a text and makes each active turtle print it
at its actual position and heading:
 If we use the list mechanism to glue together
several angles (without fixing their number), several bizarre
Logo procedures may be developed to handle and visualise such
data objects. In [5] G. Futchek describes an excellent method for
generating random mazes based on an input list of angles.
A turtle (with its pen down) will pick at random one of the
angles and turn that much right. Then it will move by fd 10 – unless the
turtle has already visited that point. If this is the case, the
turtle will pick another angle and try again, until all possible
choices (angles) were applied from all reachable points
within an area specified by a user-defined outside.area? predicate. To
implement this strategy, the shuffle
Logo primitive operation is extensively used (although Futchek in
[5] presents several clever user-specified shuffling techniques
– worth trying!):
If we use the list mechanism to glue together
several angles (without fixing their number), several bizarre
Logo procedures may be developed to handle and visualise such
data objects. In [5] G. Futchek describes an excellent method for
generating random mazes based on an input list of angles.
A turtle (with its pen down) will pick at random one of the
angles and turn that much right. Then it will move by fd 10 – unless the
turtle has already visited that point. If this is the case, the
turtle will pick another angle and try again, until all possible
choices (angles) were applied from all reachable points
within an area specified by a user-defined outside.area? predicate. To
implement this strategy, the shuffle
Logo primitive operation is extensively used (although Futchek in
[5] presents several clever user-specified shuffling techniques
– worth trying!):

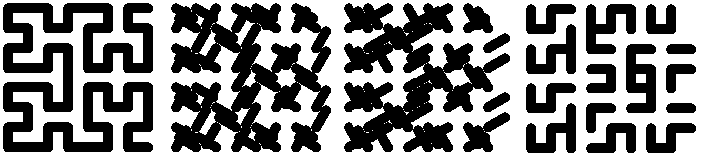

 to change.age :it
to change.age :it 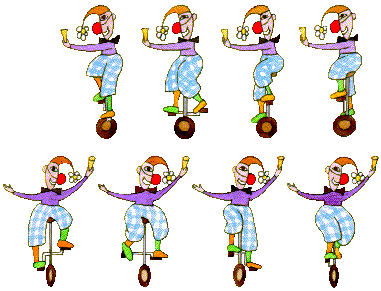 Tomash created above is an
animation turtle. As an alternative to basic turtles, animation
turtles allow us to change the frames of their shapes at any time
with the setframe
command. However, when we obtain or create nice multiple-frame
images depicting complex movements of a character in all possible
directions, we have to somehow control the turtle’s
trajectory around the screen, i.e. we have to represent a kind of
animation agenda to specify the exact headings of the
movement, basic steps, shapes and frames of the turtle etc. Such agenda
may be a list of the form:
Tomash created above is an
animation turtle. As an alternative to basic turtles, animation
turtles allow us to change the frames of their shapes at any time
with the setframe
command. However, when we obtain or create nice multiple-frame
images depicting complex movements of a character in all possible
directions, we have to somehow control the turtle’s
trajectory around the screen, i.e. we have to represent a kind of
animation agenda to specify the exact headings of the
movement, basic steps, shapes and frames of the turtle etc. Such agenda
may be a list of the form:
 Therefore,
if we create a planet with its home position in e.g. [150 0] and its shape
being item 2 :planets,
then to let it rotate forever around the origin we just say forever [setpos 1 / pos].
If we create 20
turtles named 1, 2 … etc. at the
same position [150 0],
by saying forever [each
[setpos who / pos]] we let them rotate at different
speeds. We can also let one turtle (the Moon) rotate around
another turtle (the Earth) which rotates around the origin (the
Sun). We can easily specify two different speeds as two inputs
for Eart.and.Moon
command:
Therefore,
if we create a planet with its home position in e.g. [150 0] and its shape
being item 2 :planets,
then to let it rotate forever around the origin we just say forever [setpos 1 / pos].
If we create 20
turtles named 1, 2 … etc. at the
same position [150 0],
by saying forever [each
[setpos who / pos]] we let them rotate at different
speeds. We can also let one turtle (the Moon) rotate around
another turtle (the Earth) which rotates around the origin (the
Sun). We can easily specify two different speeds as two inputs
for Eart.and.Moon
command: