LOGO: A mathematical message
Gabriela González A., Marina Kriscautzky
L.,
Patricia Martínez F.
Cómputo para Niños, DGSCA - UNAM
Ciudad Universitaria,
Distrito Federal, México
tel: 622-85-47
fax: 622-80-43
email: mkriscau@servidor.unam.mx
Abstract
In the following paper we present the usage of LOGO as a tool for the designing of didactical situations in teaching mathematical content of the first grades of primary school. We also emphasize the advantages that LOGO presents in working with deaf children.
1 Introduction
These days there exists a wide variety of software being used for many purposes. Accelerated development of technology has made possible the creation of programs that integrate some very attractive elements such as: complicated graphics with an ample gamut of colours, photographs, videos and sound which make the handling of and the interaction with the computer more and more accessable.
Seen in this way, educators have many options to chose from; however, chosing is not an easy task. To select the appropriate software, it is necessary to have a clear teaching focus which orients the actions that take place in the classroom. In this way one is equipped to make an adequate selection of tools which will aid in working toward this teaching focus.
"To think in the use of information in the school is not to think in the computer as technology, but rather in the manner in which it can help promote a learning process."
Although there are many different varieties of software with attractive designs and tools we cannot guide ourseves by the palpable of technological advances but rather it is essential to evaluate the educative power of the tool. For this reason we believe that LOGO will never go out of style. Even in its simplist versions it is a powerful tool to promote important knowledge building in children.
In the work we do with deaf children, we do not have the opportunity to work with very powerful equipment such as Microworlds and other programs technologically very advanced. But we have what we need: a rudimentary version of LOGO in Spanish.
In LOGO there are two central aspects that interest us:
The richness of LOGO is advantageous for whatever child, as all of them learn through drawing, committing errors, trying out new strategies and facing new challenges. Nevertheless, hearing children count on many other elements that they obtain through the hearing channel, whereas deaf children do not have this option. With deaf children it is necessary to exploit the visual channel to its greatest potential. Facing this lack of hearing, sight converts itself into a fundamental medium for these children to be able to relate to the world that surrounds them, to amplify their knowledge and to learn to communicate.
The graphic enviroment of LOGO is useful to motivate the child and captures his attention, but the most important aspect is that it provides the child with an immediate visual feedback after the execution of each command. This permits the child to make his own decisions, to advance at his own pace and analyze for himself his errors and correct them, without depending constantly on the teacher. In this way the computer promotes the autonomy of the child.
In addition, LOGO offers the deaf child a code, a lenguage that he can easily learn and that is effective in communicating with the turtle and carrying out projects. This is important because a deaf child’s greatest difficulty is the achieval of effective communication.
From the investigation that has taken place in the didactics of mathematics from a constructivism stance, we know that "... mathematics should be, for its students, a tool that they recreate and that evolves in facing the task of solving problems. (...) Consequently, mathematical understanding and problems cannot be separated. It does not deal with the ‘learning’ of mathematics and afterwards the ‘application’ to resolve problems but rather the learning of mathematics upon solving problems. "
For mathematical concepts to make sence to its students, it is necsessary to design didactical situations that permit them to take posetion of a concept. This is achieved by proposing problems, in which the children see the concept being taught, as the best way to solve the problem. The concept adquires significance when it is useful to resolve a problem. Upon designing a didactical situation, one must be sure that the concept being taught appears to the students "...as a medium to select, anticipate, execute and control the strategies that apply to the resolution of the proposed problem ..."
Inside a didactical situation we have numerous variables or conditions that can favour the adquisition of knowledge by affecting or modifying the procedures that the students use to solve this problem. We call them didactic variables because through working with them, we can evolve the strategies that the students use, so that the knowledge to adquire is the most efficient medium to resolve the proposed problem. Through the manipulation of these variables we promote the construction of new knowledge. The knowledge is no longer a finished product as it becomes evident the process of its construction. Conventional knowledge as it is found in its actual state of knowledge, is the final process, the point of arrival and not the point of departure. The children can reconstruct the evolution of knowledge in the same way in which it is produced: resolving problems or facing challenges that men have planted in various moments of history.
In our selection of mathematical content of the first years of primary school, we have decided to work with numbers and mearusing in didactical situations in the LOGO environment. To propose good problems is a challenge for educators. We think that the communication of quantities through LOGO is a good problem, a challenge that promotes the construction of knowledge.
We have designed a situation that consists in copying a figure using the commands of LOGO. In this case the copying is not a mechanical task as it is necessary to make be aware of the implied actions in the realization of the drawing in order to be able to communicate them to the turtle. For this reason we say that with LOGO we make mathematical messages, we communicate quantities using the numerical system and the language of the turtle. This situation permits the construction of the concept of numbers. This appears to be the medium to be able to realize the message in an effective form. Through the manipulation of its variables, the situation also permits the generation of other didactical situations to be used in the teaching of this concept. Situations in which the problems are resolved using the numbers with their different meanings.
In the didactical situations we can identify some characteristics that help us to decide if they are "good problems" or not. Let us look at the characteristics of the mathematical message with LOGO. When we ask a child to copy a figure in the most exact possible manner in the computer, we are not requesting a mechanical action. We are proposing a challenge for which the child should develop strategies and put them to the test. This is the principal characteristic of a didactical situation.

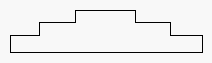
Figure 1 A cake made in Draw. The design is realized on graph paper.
To copy this cake implies that one must obtain the correct measurements and communicate them to the turtle. It is necessary to count the squares and note them or memorize the quantities in order to afterwards be able to execute the command "A" (advance) the same number of times. Upon communicating a quantity the concept of number is put into play. If one makes a mistake, the turtle will make a cake, but not the one that we wanted.
In the case of non coincidence, the children themselves have to where the error took place: in the initial count or in the message. The turtle’s interpretation shows the result of the action. In dealing with deaf children, this feedback is fundamental as there is no need for an evolved language to be able to reflect upon the actions. In another way the delay in linguistic development becomes an obstacle for the adquisition of mathematical notions.
We have to plan the actions in order to be able to obtain what we desire, to make decisions and to have "...the possibility of knowing directly the conscequences of these decisions with the purpose of modifying them, to make them adequate upon the achievement of the persued goal." The situation itself lets us verify our hypothesis, without depending on the judgement of the teacher as the only available source of feedback. This is another one of the characteristics of a good learning situation.
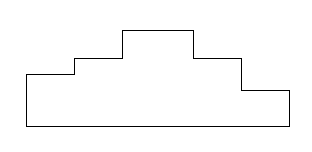
Figure 2 Cake made by Diego
To respond to this challenge the children can use diverse strategies and different procedures to resolve the problem. This is another characteristic of a "good problem".
Finally a didactic situation should permit the production of other situations through the manipulation of its variables "blocking the use of some strategies and generating conditions for the appearance and stablization of others (underlying the concept that is being taught)."
Moving away from this base situation, we designed other situations which through the modification of one or many variables we provoked an evolution in the procedures used by the children as it became necessary to use new concepts to be able to solve the problem. The selection of variables that are transformed obeys the type of knowledge that we want to teach and the procedures that we try to evolve in the children. In this way, starting from the same situation (copying a drawing with the turtle as an intermediate and using its language) various concepts are put into play. In the anterior example we saw the notion of numbers in action. In that example it was not necessary that the children know how to count up to many numbers as they would solve the problem with a rudimentary count. Upon passing to the next level (park) the situation was made more complicated. One cannot count while executing the action. It is necessary to anticipate the measurements and express them conventially using the number system. In this version, the mathematical message implies larger quantities and the writing of the decimal system. There also appears the notion of ‘turn’ which in the anterior situation was not relevant. In this case it is necessary to decide beforehand in which dirrection to turn. The measurement of the turn can be learned by memory as it is not a problem the necessary involves the concept of angle.
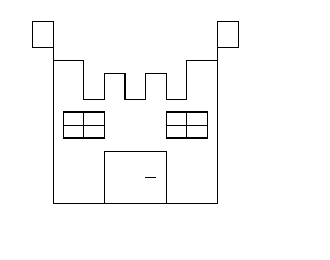
Figure 3 Castle, on graph paper.
If we take away the graphs from the paper, the problem becomes more complicated: one must check with precision the measurements and to do this it is necessary to use instruments of measurement like the graduated ruler.
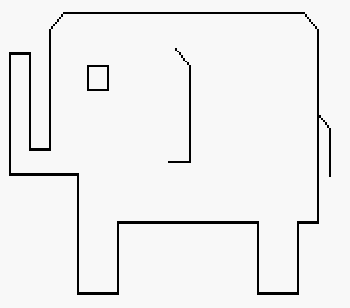
Figure 4 Elephant on blank paper.
Also we can leave out some measurements that can be calculated for the children using procedures that involve addition and subtraction.
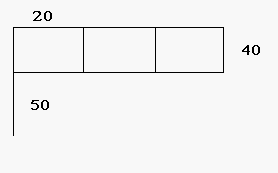
Figure 5 Flag
And if now we introduce diverse turns we impede that they calculate memorizing the instruction of 90 degrees to the right or 45 degrees to the left. It becomes necessary to check the measurement of the turn. Once again the use of measurement instruments are required like the protractor. The notion of angle starts to build itself in the resolution of this problem.

Figure 6 Guitar
We can make the situation even more complicated by introducing other angles and perfecting the measuring instrument. Also we can direct it towards other concepts like ratios, requiring for example that the coppied drawing results 1/3 the size of the original.
With these brief examples we want to show that LOGO is a very important tool in the design of didactical situations where the children can build their knowledge and not recieve it as if it were a finished product. Situations where the children themselves achieve putting their knowledge into action to be able to solve problems. In our opinion the LOGO enviroment on its own does not promote these situations. It is necessary to design situations that permit significant understandings. LOGO is an excelent option, especially if we think about deaf children who need more than anything, a visual reference for their actions.