One approach to mechanic
simulations in Logo
K. Alexandrov, S. Soprunov
Institute of New Technologies of Education
10 Nizhnaya Radishevskaya,
109004, Moscow, Russia.
tel: (7095) 915-1394,
fax: (7095) 915-6963,
email: soprunov@glas.apc.org
Abstract
We discuss an extension of MicroWorlds (LCSI) software for kinematics and dynamic simulations. For the kinematics simulations we consider turtles as living on different "glass planes" and extend MicroWolds with few new primitives that help user to describe turtle motion in different frames of reference. For the dynamic simulations we add a tool that allows user to describe turtle behavior in the terms of an acceleration field.
Keywords
Simulation, kinematics, dynamic, MicroWorlds
1 Introduction
The idea of using Logo turtles for simulation of motion of real physical object looks quite natural (e.g. the Dynaturtles, [3] pp. 122 - 124). The MicroWorlds (LCSI) software environment fits for such kind of simulations perfectly due to the number of turtles, independent parallel processes, etc. So we made an experimental extension of the MicroWorlds software to simplify kinematics and dynamic simulations.
In this paper we use MicroWorlds dialect of Logo [2]. Fortunately, we will rarely need more complicated language constructions then fd, bk, rt, forever, and so on.
2 Kinematics
The standard metaphor for Logo is: the turtles live on a plane (on a torus, more precisely) and they can move on the plane under instructions. It is not the only metaphor that can be used: we can consider, for example, the computer screen as a window looking out onto turtles in a three-dimensional world [1] p. 144. Then under this metaphor we need new instructions to maneuver turtles in a 3D-space.
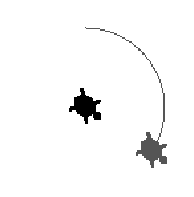
Let us imagine now that each turtle lives on its own transparent plane so all movements (forward, right and so on) turtle makes relatively its plane as a frame of reference. It does not differ from the standard metaphor as long as planes remain motionless. But let us suppose that we can tie firmly (with a new Logo primitive) a plane of first turtle as a rigid body to a second turtle. Now a movement of second turtle will move the plane of the first one and, as result will move the first turtle itself. In other words, we extend MicroWorlds Logo language with a new primitive stick_to turtle-name with the following semantics: command stick_to turtle-name glues the plane of the currently active turtle to the turtle turtle-name.
Let us consider the following example: there are two turtles with names gray and black. Then after the instructions:
gray, pd stick_to "black
black, forever [right 1]
the gray turtle draws a circle:

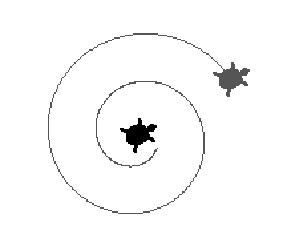
In the previous example the gray turtle stays motionless (relatively its plane), but we can ask it to move also, certainly. If we add the line
gray, forever [forward 0.1]
to the previous instructions then we get a spiral motion:
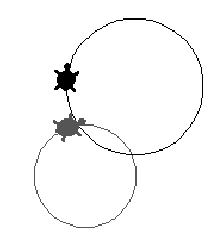
We would like to add one more example to brighten up the stick_to primitive semantic. It's obvious, that the instructions:
gray, pd stick_to "black forever [fd 1 rt 1]
black, forever [fd 1]
will draw a cycloid -- the path of a wheel rim point:

We can certainly create a more complex turtle system sticking one turtle to a second one, second turtle to a third one and so on. Here is an example: on the next figure the both black turtles are running instruction forever [rt 1], the gray one is running instruction forever [lt 2]. The gray turtle is stuck to the big black one, the small black turtle is stuck to the gray one. The distance (d) between the big black turtle and the gray one is equal to the distance between the gray turtle and the small black one, so the small black turtle makes simple oscillation 2ĚdĚsin(t). The big black turtle is stuck to the tractor that drags the whole system along a screen running instruction forever [fd 1]:

It's easy to see that we can take other three turtles to describe an oscillation with some amplitude and frequency, stick the new system to the small black turtle and observe the sum of two oscillations and so on.
We can summarize the stick_to extension in more scientific terms: the primitive stick_to allows us to describe a motion of an object in a frame of reference, describe a motion of the frame of reference and then observe the resulting motion in the absolute frame of reference.
We can consider the dual problem: we describe motions of few objects in the absolute frame of reference and after it we would like to observe the motions in a frame of reference tied to one of the moving objects, in another words we would like to observe the motions of all turtles from the "point of view" of one of them. To realize this approach we add the transfix primitive. The transfix primitive has no parameters, it switches our screen from the absolute coordinate system to the active turtle point of view. Let us consider examples.
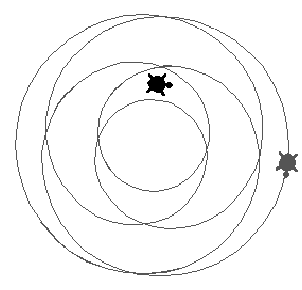
On the next figure the gray turtle is running instruction forever [fd 3 rt 4], the black one is running independently instruction forever [fd 10 rt 10]:
Here are just the same motions seen after gray, transfix instruction (from the gray turtle point of view):

and after black, transfix instruction (from the point of view of the black turtle):
Let us recall an old problem: there are 4 turtles (t1, t2, t3, and t4) in a square vertexes. They start to run at the same time keeping heading on a neighboring turtle (e.g., the turtle t1 starts to run instruction forever [towards "t2 fd 1] and so on). The question is: when they will meet?
Here is the motion of turtles in the absolute coordinate system:

and from one of four turtles point of view (after transfix instruction):
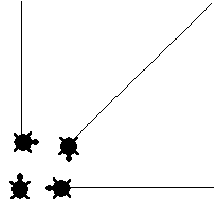
Now the answer is almost obvious: we notice that the heading of the transfixed turtle and a heading of another turtle are mutually perpendicular, so the mutual approaching speed is equal to the speed of one turtle.
3 Dynamic
For a simple dynamic simulation it is useful to consider Logo turtle as a physical object with velocity and mass. In our approach we would like to allow user to describe (in the Logo language terms) a force function for a turtle system and observe a behavior of the system.
To simplify this kind of simulations the following changes were made in the standard MicroWorlds: we add tools for turtle initial velocity and mass settings and added new special word field to the MicroWorlds vocabulary. Field is a special name for a procedure that describes a force function (more precisely, an acceleration field function) on pages of a project. A field procedure has to be reporter without parameters and it has to report a two-dimensional vector: a list that contains two numbers. These two numbers determine x-coordinate and y-coordinate of acceleration (velocity changing). If there is a procedure named field on the Procedures page, then the software considers the procedure as a rule for acceleration calculation and applies this rule to all turtles on a current page.
Let us consider a simple example. Let us have the following procedure on the Procedures page:
to field
output [0 -0.01]
end
and 2 turtles on a current page with different initial velocities. Here are the resulting motions:
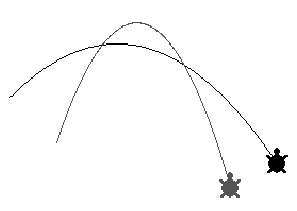
If we "look inside" the software we certainly find an infinite loop that looks over all turtles on a page, checks and changes their velocities, moves them on the screen and so on. So the software simulates turtle motions in a very natural standard way. The advantage of the proposed approach is that user does not need to care about all these details. A simulation process is running implicitly and user needs only to describe explicitly a rule of simulation.
Describing forces on a plane we need usual two-dimensional vector operations like addition, subtraction, magnitude, and so on. So we add more or less standard vector manipulation library to the MicroWorlds Logo language. We will underline these library vector operations in procedure texts. In our next examples we will need the following library procedures:
v-sum vector1 vector2.
Reports the sum of two plane vectors.
v-diff vector1 vector2.
Reports the difference of the plane vectors.
v-unit vector.
Reports the unit vector with the same heading as the argument vector.
v-magnitude vector.
Reports the length of the argument vector.
v-mul number vector.
Reports the result of multiplication of the number to vector.
Our first example was very simple; the field procedure reports constant vector in fact. Here is a more complicated example. We would like to simulate a simple pendulum connected with a spring. In this case the resulting acceleration is a sum of two vectors: a constant vector of gravity acceleration and a vector of acceleration from spring. The heading of the last one coincides with the heading of the spring, the magnitude of the vector is proportional to the difference between current spring length and a standard spring length. Let us try to write the procedures:
;field reports the acceleration vector as the sum of
;the constant vector [0 -0.1] and a vector reported by
;the procedure spring.
to field
output v-sum [0 -0.1]
spring [0 100] 100 0.04
end
;spring takes 3 parameters: coordinates of the point to which
;one end of spring is attached, a standard length of the
;spring, and coefficient of the spring elasticity.
to spring :point :standard :coeff
let [spring-vector v-diff :point pos
;the spring vector is the vector difference between the
;end of the spring and the turtle current position
direction v-unit :spring-vector
delta (v-magnitude :spring-vector) - :standard]
output v-mul :coeff * :delta :direction
end
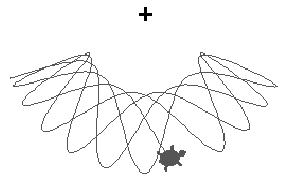
In our last example we will try to describe the motion of two planets. Let us take two turtles named earth and sun. As we mentioned above we can set "a mass" of a turtle, so we will make the sun turtle twice heavier then the earth one. Now we are ready to describe the gravity acceleration:
;field
reports the acceleration of an active turtle.
to field
if who = "earth [output gravity "sun
"earth]
if who = "sun [output gravity "earth "sun]
end
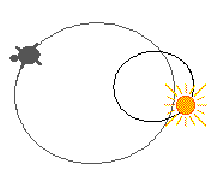
On the next figure we can see just the same motion from the earth point of view (after earth, transfix instruction) if the earth is running in parallel the process forever [rt 3]:
References