Mathematical microworlds
with a variation tool
in a Component Logo environment
Siouti X., Trouki E., Psycharis G.
University of Athens, School of Philosophy,
Dept. of Philosophy,
Education and Psychology, Section of Education
Panepistimiopolis, Ilissia,Athens, Greece,
tel: 7248118, fax: 7248979
email: psiouti@cti.gr
Abstract
In this poster we discuss mathematical microworlds based on a Component Logo environment enriched with a tool for manipulating variation. During the session we will present: a) a small number of mathematical microworlds, b) a case study of 11 year old pupils’ understanding of triangles and similarity and c) a case study of pupils’ verbal communication while using the tool in a classroom ‘angle’ project. The presentation will consist of pupil dialogues and microworld ideas in hardcopy form and the opportunity for exploring with the microworlds and browsing through pupils’ work on a computer.
Keywords
microworlds, dynamic representation, triangle, variation
The Component Logo environment [2] provides components, i.e. reusable entities of a variety of technical complexity (e.g. a map, a compass, a turtle) each designed so that it can interoperate with a range of other components [4]. A language based on MSW Logo is a key feature of the environment providing Logo’s functionalities and a scripting mechanism to link and operate components. The variation tool can only operate when linked onto other components which have parametric behavior. It provides a kinesthetic metaphor for manipulating ‘continuous’ change of a parameter and the component’s resulting behavior.
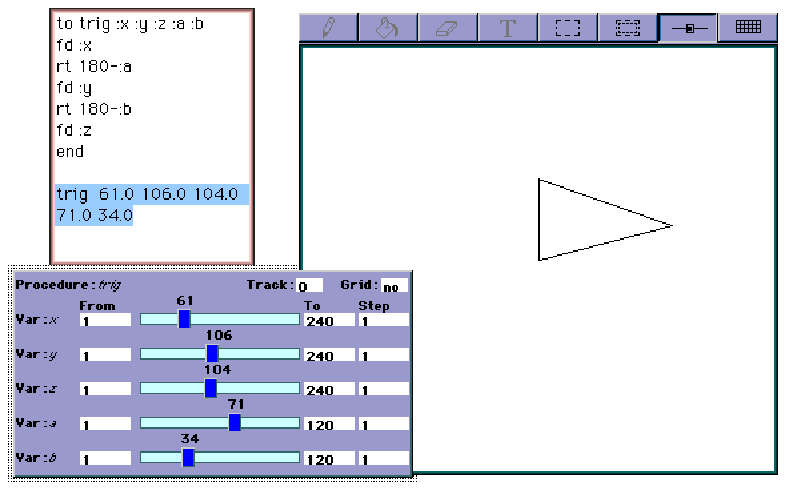
The integration of the variation tool within a programming language (Logo) gives educators the chance to try out new ideas for designing mathematical microworlds (see figure below). One group of ideas is procedures creating traditional geometrical representations which can be used or changed and studied by pupils. Pupils thus have a mathematical construct which they might use either as a tool by observing the effect of moving the variation tool or as an object by changing and studying it. So, they can discover through exploration and observation interesting geometrical and algebraic properties of such mathematical objects[1], [2].

The variation tool in a Turtle Geometry setting
Another group of such ideas could be the simulation of physical motion (animation) such as the movement of a clock’s hands, the flapping of a bird’s wings etc. In this case pupils are encouraged to construct mathematical models of motion expressed in a programming language. Motion can be controlled and manipulated through the variation tool giving opportunities for further exploration of its mathematical variables. As a result, pupils explore the mathematical relations among properties which are embedded in the simulation [2].
The case study we present involved two 11 year-old pupils. They were asked to construct equilateral triangles of different sizes. They finally constructed an equilateral triangle using only one variable for its sides. That had the effect of a growing and shrinking triangle. Even though the analysis of the results is on-going, we present some points of interest, such as that the pupils:
As far as communication is concerned, a point of interest is pupil discussion regarding the simultaneous kinesthetic, graphical and formal representation of variation caused by manipulating the variation tool. Another is the rich opportunity to exchange ideas and appreciate the necessity of reasoning and forming well-argued proposals in order to participate properly in a discussion, encouraged by the continuous feedback effect of manipulating parametric constructions. Situating such learning environments in the Greek educational system where collaborative learning is far from encouraged, provides an interesting framework for interpreting such findings as a process of infusing innovation in school practice[3].
References