Bringing LOGO to the World of
Purely Functional Programming
Zoran Putnik, Zoran Budimac
Institute of Mathematics, Faculty of Science,
University of Novi Sad
Trg Dositeja Obradoviã
4,
21000 Novi Sad, Yugoslavia
email: putnik@unsim.ns.ac.yu,
zjb@unsim.ns.ac.yu
Abstract
Turtle graphics has been implemented in a purely functional programming language. The implementation is easily portable to any purely functional programming language that has limited graphics capabilities. The main importance of the implementation is in its educational value. The implementation brings the expressiveness of LOGO to functional programming.
Keywords
Turtle Graphics, Functional Programming, ISWIM
1 Introduction
Because both graphics and functional programming are very useful in teaching programming in introductory courses, the two were combined in the same functional language. This paper describes a pure functional implementation of turtle graphics. The implementation is referentially transparent and it is not based on side-effects and assignment statements.
2 Preliminaries and Related Work
Since the invention of programming language LOGO, turtle graphics has been recognized as a suitable educational tool, especially for a development of procedural thinking. The implementation of turtle graphics in a purely functional programming language is important because of its twofold educational value. It shows:
Our solution is based on the algorithms given in [5]. Although the solution appeared as purely functional to an end-user, it was indeed based on a state, which was destructively updated after every turtle action. Besides "impurity," other flaw of this implementation was its dependence on the special language features. One purely functional implementation of turtle graphics functions is described in [3] and is based on a list of commands, which are to be interpreted in sequence. Every command takes a previous turtle state and returns a new state, giving a "description" of turtle action between the two states. The result of an interpretation of a command list is a list of descriptions of turtle actions.
Implementation described in this paper combines the good sides of both approaches, by taking the "interpreter" approach from [3], while is essentially based on a set of turtle functions introduced in [5]. This paper is the extension of [2].
3 On Programming Language
The implementation of turtle graphics functions is given in ISWIM/NS (an ISWIM-like programming language) and is easily portable to every other purely functional programming language. To port this solution to the other purely functional programming language, one needs only two "unusual" operators:
Both operators are easy to implement in most purely functional programming languages. Therefore, we regard our solution as easily portable. The implementation and usage of ISWIM/NS used in this paper is described in [4].
All turtle functions will be defined in a separate library file turtle. Function definition f is imported from the library file turtle as: f from turtle. The call of the primitive function seq(a,b) returns the value of b, previously evaluating a. The call of function line(x, y, x', y', c) draws a line from coordinates (x,y) to (x',y') in color c.
4 Turtle Interpreter
The function once takes a list of turtle commands comm and the current turtle state and sequentially applies every command from comm to a state. It is expected that every turtle command is defined such that:
Function call once(comm)(state) repeatedly applies commands from the list comm to the state, producing the new state. The function repeat repeats once n times:
repeat(n, comm)(state) = { n <= 0 -> state;
repeat(n-1, comm) (once(comm)(state)) where rec
once from turtle }
One additional function is useful: the function turtle simply calls the function once with supplied initial state.
5 Turtle Commands
As already noted, every turtle action besides other arguments, must take a turtle state as an additional argument and must return a turtle state as its result. The state must be the last argument of every turtle action and must be separated from other arguments. Most frequently used turtle actions are provided in the function library turtle. All of them will be described in this section.
Functions up and down set the position of turtle pencil to "up" and "down" respectively. Function angle sets the current angle (direction) of the turtle to the given one. The function home sets the turtle into its initial position (center of the screen, looking up with the pencil down). Function turn changes the current turtle angle for n degrees (modulo 360). As an example, we give the implementation of the command up :
up(state) = [state!1, state!2, state!3, "up"]
Function jumpTo moves the turtle to new coordinates (x,y), while function drawTo draws a line form current to given coordinates. Both functions change the turtle state. The implementation of jumpTo is as follows:
jumpTo(x,y)(state) = [x, y, state!3, state!4]
Function forward draws a line of a given length in a current turtle direction as follows:
forward(n)(state) = {{ let x1 = state!1 and
y1 = state!2 and
ag = state!3 and
pl = state!4 and
kk = 57.29578 ;
{ let x = x1 + cos(ag/kk)*n and
y = y1 + sin(ag/kk)*n ;
pl = "down" -> drawTo(x,y)(state);
jumpTo(x,y)(state)}
} where rec
jumpTo from turtle and
drawTo from turtle }
6 Example
The following program draws a picture displayed in figure (captured from the screen). Note that the turtle state is not visible, because the program is completely based on turtle library functions, which are curried in their last argument. Therefore, we always call library functions without their last argument (the turtle state). The turtle state is "carried around" by library functions, and we do not care about it in the main program.
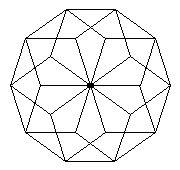{ spider where rec
spider(n) = turtle([repeat(10, [five(n), turn(36)])]) and
five(n) = repeat(5, [side(n)]) and
side(n) = once([forward(n), turn(72)]) and
forward from turtle and turn from turtle and
turtle from turtle and once from turtle and
repeat from turtle }
References